European versus American Roulette in Figures – Which Wheel Favors the Player

Author: Dr. Catalin Barboianu

Every classical game of chance has evolved in more or less popular versions over time, and roulette is not an exception. During its history, roulette has undergone some modifications to the wheel or table layout, including the number of numbers as its outcomes. Two versions have remained extremely popular today, European, and American roulette, followed by French roulette.

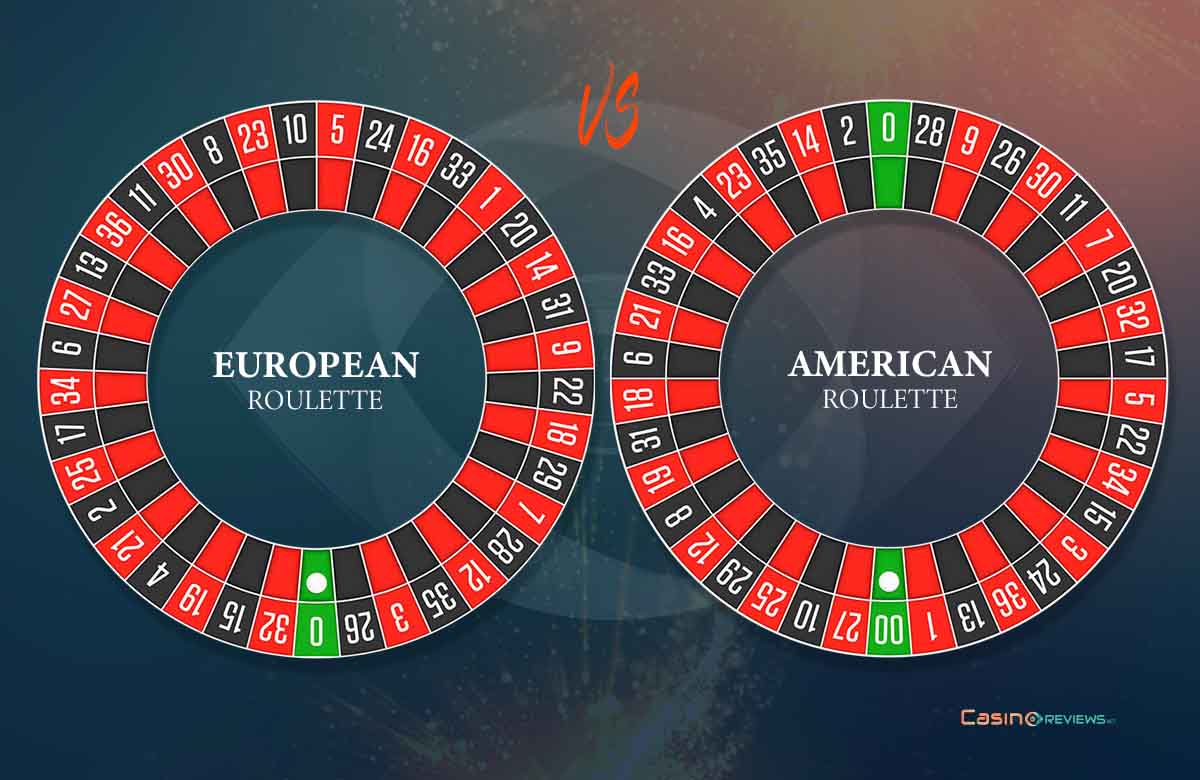
The Zeros of Roulette

European roulette adds a zero to the usual 36 numbers of the mother version invented by mathematician Blaise Pascal in the 17th century. Of course, this modification (made in the mid-19th century) was intended to favor the house, as the conventional number zero is not included in the outside bets (red, black, odd, even, etc.). Still, in the 19th century, as roulette was spreading quickly in America, it has not escaped American influence and obtained a new conventional number, the double zero, to make the house advantage even bigger while keeping the same payout schedule of the European roulette.

French roulette keeps the same numbers, layout, and payout schedule as the European roulette. The difference consists of two additional rules in effect when you place an outside bet and zero lands: in this case, your bet is either kept for an extra spin (En Prison) or returned in half amount (La Partage). These rules change the house edge to 1.35% when they apply. For the rest of the situations, the same house edge of 2.70% stands as in European roulette, and all the mathematical parameters of the bets are the same for the two roulette versions.

We will then analyze the differences between European and American roulette in terms of what concerns the mathematics of roulette betting.

Differences in Probabilities and Expectations

Just a single number added on the wheel (the double zero) almost doubles the house edge, that is, 5.26% for American roulette compared with 2.70% for European roulette. This seems like a major advantage of the former over the latter from a player’s point of view but remember that house edge is defined in terms of profit or expectation over an indefinite period as a statistical mean. If we think just in terms of probabilities of winning the bets in a game, the difference will still favor European roulette but not so significantly.

Indeed, for a straight-up bet, the difference in probability of winning is 1/37 – 1/38 = 0.00071 = 0.071%, which one may consider negligible and not take into account as a criterion for choosing European roulette.

The difference gets higher with the coverage of the bet: for a street bet, 3/37 – 3/38 = 0.21%; for a line bet, 6/37 – 6/38 = 0.43%; for a dozen bet, 12/37 – 12/38 = 0.86%, attaining its maximum for a color, even/odd, or low/high bet, namely, 18/37 – 18/38 = 1.28%. It is still not much, but these latter types of bets are those mostly affected by the zero and double zero, and for American roulette, the chances of losing such a bet are almost doubled (2/38 versus 1/37, in fact, the two-house edges, 5.26% versus 2.70%, respectively).

Regarding the probabilities of winning, that 1.28% difference gets even higher for combined bets with high coverage. For instance, a combined bet consisting of a bet on a color and 17 equal straight-up bets on numbers of the opposite color (assuming the stakes are such chosen for the bet not to be contradictory) has a probability of winning (landing either on the color or on a number among those chosen) of 94.59% in European roulette and 92.10% in American roulette, and the difference is 2.49%.

Regarding the probabilities of winning, that 1.28% difference gets even higher for combined bets with high coverage. For instance, a combined bet consisting of a bet on a color and 17 equal straight-up bets on numbers of the opposite color (assuming the stakes are such chosen for the bet not to be contradictory) has a probability of winning (landing either on the color or on a number among those chosen) of 94.59% in European roulette and 92.10% in American roulette, and the difference is 2.49%.

For instance, a color bet with a stake of $20 in European roulette has an expectation of –$0.54, while the same bet has an expectation of –$1.05 in American roulette. That is, you are mathematically expected to lose 54 cents for every $20 color bet in the former case and $1.05 in the latter; again, almost twice. Since you may use that difference in money lost to place a new bet instead, it clearly turns into an advantage of European roulette.

A Small Exception in Repeated Bets

Seeing that all these basic odds and means favor European roulette, is there anything that this roulette version might be surpassed by the American one? Our previous analysis was made for individual bets placed within a game, that is, one spin. What happens if a bet is repeated over a series of spins?

First, if we think of winning that bet several times in a row, the probability of such event is calculated as a power of the probability of winning the bet in one game (probability of winning raised at the power being the number of consecutive spins in that series); for instance, a column bet (with a winning probability of 12/37 in European roulette) is won for three times in a row with a probability of . The corresponding probability in American roulette is , which is obviously lower than the previous.

For this kind of event, nothing changes with the order between probabilities for the two versions of roulette. Indeed, whatever bet is considered, raising two numbers (probabilities) at the same power preserves the order of those numbers. Therefore, European roulette remains the favorite.

Things change a bit if we formulate the event to be measured in probability by asking for an exact number of winnings over a given number of spins, for example, in the case of a repeated color bet, “exactly three reds in ten spins” and the like. The probabilities of such events follow what we call a binomial distribution. For example, remaining at the color bet, say black:

The probability of a black number occurring only once in 10 spins is 0.0146 (1.46%) in American and 0.0120 (1.20%) in European roulette; the order in favor of American roulette remains for exactly two reds (5.94% versus 5.14%), exactly three reds (14.26% versus 13.00%), exactly four reds (22.47% versus 21.56%), until five reds, where the balance inclines back to European roulette (24.27% versus 24.52%) upward to 10 reds (0.05% versus 0.07%).

This probability has a similar behavior for longer series of spins but not for any kind of bet: for example, for a dozen bet, only the probabilities for 1, 2, and 3 hits are higher in American roulette; for a line bet, only for one hit is higher, and for bets with a coverage lower than 12 numbers, all are less than those in European roulette.

In our example, is the comparison of those initial probabilities (of hitting 1, 2, 3, and 4 blacks in 10 spins) of any relevance in choosing American roulette, or is it just a mathematical curiosity? Adding them up, we understand that the probability of hitting at least one and at most 4 blacks in 10 spins is higher in American roulette (with a difference of 3.23%). Meanwhile, if we consider the probabilities of hitting at least 6, 7, 8, or 9 blacks in 10 spins, they are all higher in European roulette (with the difference within a range up to 3%). These results apply symmetrically to the betting on the color red and also to other similar outside bets (even/odd, etc.).

Players using progressive betting systems such as martingale might find this information interesting. Those who keep betting on the same outcome over their progression do not want long series of reds or blacks and the like and may turn to American roulette just for the higher probability of having up to 4 outcomes of the same kind in 10 spins. Those who switch their bets during their progression (red to black and conversely) can no longer base their choice on such criterion since a switch may synchronize with the switch of the outcome from favorable to unfavorable.

Conclusion

All this mathematical fact is a merely theoretical advantage of American roulette with a narrow application. In practice, this advantage is so small that it dissipates easily. First, those differences in probability for repeated bets are not high and get annulled and even reversed in terms of the real frequencies of the outcomes over the short to medium run. Second, it is unrealistic to assume that a martingale player does not place regular (nonprogressive) bets as well from time to time or even more often, and for such bets, the advantage of the European version is dominant.

Overall, the figures associated with the bets in a roulette game favor the European version, so why would a player choose the American version? The only practical reason for such a choice would actually fall outside the mathematical results, in the casino’s particular rules applied to betting in that game. One of them would be the existence of American roulettes allowing lower stakes for particular types of bets.