The Hidden Math of Slots – Configurations, Combinations and Facts about Slot Games

Author: Dr. Catalin Barboianu

For decades, the slot game has remained one of the most popular games of chance. Beyond variety, brevity, and privacy as the main elements that contribute to this position, there is also the attractive physical design—from the graphics of the symbols to the design of the interface and even case, all is sparkling and brightly colored. However, there is another kind of design that characterizes slots and is of utmost importance for the developers and operators of slot games, namely, their mathematical design.

The Mathematical Configuration of a Slots Game

When a slots game is designed mathematically, the basic process starts with assigning symbols along with a symbol distribution (the following to be determined) on separate sets of indexed stops, forming the “reels.” The distribution of the symbols is then determined mathematically such that the probabilities of the winning combinations and some statistical indicators fit the developer’s goals.

The general mathematics of slots is not that advanced despite the fact that a slot is a combinatorial game, and anyone can come to know it from various sources. Still, its application to particular games is impossible most of the time just because slots have a “bad reputation” among the games of chance, despite their popularity—the parametric configuration is usually kept secret by game producers. Let’s see what this parametric configuration means.

Each reel has a number of stops, and a number of symbols may be shown in combinations as outcomes on the paylines. These numbers (of stops and symbols) are the basic parameters of a slots game, but there are more. The configuration of a reel refers to the distribution of the symbols over the stops of that reel and the arrangement of the symbols. Each symbol is present in various instances on the stops of a reel, and these numbers of instances form a vector called the symbol weighting of that reel.

All these parameters of the reels identify a slots game and are determined by the game producer. The numbers of stops of the reels and the symbol distributions on the reels stand as variables for any general formula for the probability of a winning event defined on a payline. In its most general form, the probability of such an event E occurring on a payline of length n (crossing over n reels) is P(E) = F(E) / (t₁ . t₂. ... . t_n), where F(E) is the number of combinations of stops on that payline favorable for the event E to occur and the indexed ts denote the number of stops of each reel crossed by that payline.

The formula above is a combinatorial formula for probability since F(E) is obtained in a combinatorial framework. The probabilities expressed through the combinatorial formula above cannot actually be computed as long as the parameters of the game remain unknown. Only the game producer and his staff know those probabilities for a particular game. With this lack of input data, the parameters in that formula remain just variables.

Hit Rate and RNG

For a better understanding, we can express the combinatorial formula below in general frequential terms, complying with the usual slots jargon.

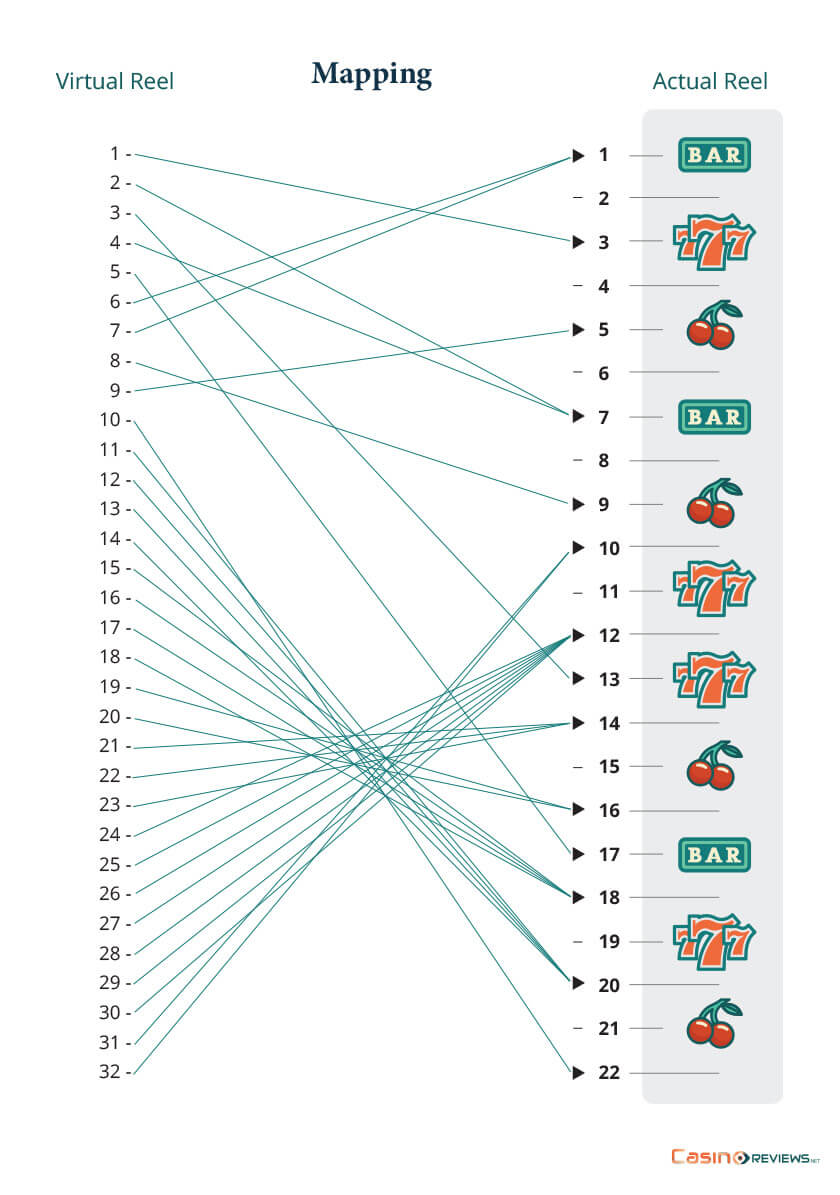
Figure 1: Virtual reel to actual physical reel - Mapping

The cycle refers to the entire number of combinations of stops that may occur as outcomes on a payline in a slots game. It corresponds to the denominator of the fraction in the combinatorial formula, namely, the product of the number of stops of the reels (the ts).

Hits are combinations of stops holding a given winning combination of symbols. Each hit corresponds to the numerator of the fraction in that formula. With this terminology, the general combinatorial formula is written as follows:

probability (of a given winning combination) = hits/cycle

The cycle is interpreted in this formula as the number of spins in which every combination of stops occurs only once, while the amount of hits is the number of occurrences of the given winning combination over that cycle.

The hit rate is the relative frequency of a given winning combination over the long run.

hit rate = 1 /probability = cycle/hits

The hit frequency is just the hit rate expressed as a percentage:

hit frequency = 100% /hit rate

With the evolution of slots, more and more symbols have been added to the reels, but classical physical reels can only hold a limited number of stops (around 22). The second generation of slot machines used physical reels for displaying the outcome, spun electronically (called electromechanical slots); however, the outcome is determined on virtual reels with a random number generator (RNG).

A virtual reel can have stops in any number, so the idea was to reduce the weighting of the symbols on the physical reel such that the reel holds as many symbols as possible and makes the actual weighting on the virtual reel. Then the virtual reel is mapped onto the physical reel (several instances of the same symbol on the virtual reel are mapped into one symbol on the physical reel by preserving the arrangement of the symbols). The RNG provides the stop to be selected from the virtual reel, which commands the physical reel to stop on the correlated physical stop. The third generation of slots consists of the video slots, where the virtual reels also display the outcome directly.

Statistical Indicators — RTP and Volatility

Employing the prizes associated with the winning combinations, we can define average win = prize × probability (of that prize) and return to player (RTP) as RTP = (average win/average bet) × 100%.

The RTP indicator above reflects the percentage of the total bet amount that the machine returns to players as prizes for hitting that winning combination over the long run (this is the meaning of “average”).

The RTP of a game is the sum of the RTPs of each of its winning combinations. For many slots games, the RTP is information exposed by either the operator or experts who studied the game. A possible reason for exposure by the operators is that most of the RTPs are percentages close to 100%, and such values of this indicator are thought to be perceived as advantageous from the player’s perspective. However, the RTP is actually 1 minus the house edge of the game, and as long as the house edge remains positive, slots look like any game of chance (except that the winning probabilities are not known or calculable). An RTP of 97% means a house edge of 3%, close to the house edge of European roulette, for instance.

In slots with progressive jackpots, the RTP with respect to the game’s spin prizes increases because of the contribution of the jackpot.

Another statistical indicator of a slots game is volatility, expressed as the variance over a definite interval of plays. Variance is a statistical indicator that measures the deviation of the data (the values of the random variable) from the mean or expected value as an average of their squared deviation. Volatility reflects how the RTP is distributed in prizes over a given number of plays—that is, how often and how big the wins are on average over that interval.

There are several scales on which volatility is measured, and the most common classification for slots games is with low, medium, or high volatility. The indicator for such measurement is the volatility index, which is defined as the product between the standard deviation and another indicator called the z-score, the number of standard deviations a given data point lies away from the mean. The z-score is associated with a confidence interval, which shows the range of the RTP after the given number of plays. These latter indicators are of most concern for the game developer, being used to test the performance of a new game in simulations.

Choose the Game by RTP—But Do Not Trust RTP Literally

The RTP of a game is a statistical indicator based on a statistical average and should not be interpreted as the return for a given player from that player’s own bets but cumulatively—that is, the return from all the players’ bets to all the players over the long run. A player is not necessarily paid in prizes from his own investment but from all the players’ bets. This is also a premise of playing slots; otherwise, no profit would be possible provided the house edge is maintained. In other words, interpreting the RTP for just one player is the return from that player’s investment to that player if they play that game an infinite number of times.

In slots, the only strategy is that of choosing—choosing what game to play, for how long, how many paylines to enable, whether to multiply your bet or not and so on. There is also minimal organization available, namely, the bankroll management with respect to the games chosen and the intended playing time. The first criterion of choosing a slots game is clearly the RTP, if this information is available—the higher the RTP, the better. Usually, online slots have higher RTPs than those in physical casinos because the latter are assumed to have more expenses with their business than the former.

If you know the RTP of a game, keep in mind that that payback is not materialized over a given time or number of spins; it remains a statistical average assuming an infinite number of trials.

Fallacious Beliefs Related to Payback

Misinterpreting the RTP with regard to the payback is not the only misconception that the players frequently have about slots. In addition, every spin is independent of any other, and the outcomes are randomly chosen by the RNG. The RNG picks a random number for each reel, with each number matching a stop on that reel. Then the machine directs the reels to stop on the spots indirectly selected by the RNG.

By the time the reels are spinning, the game is already over, as the RNG has already selected the stops. The reels spin sort of as a courtesy to the player but also to induce some psychological effects advantageous for the operator. In fact, electronic slot machines don’t even need visible reels since the outcome is determined spot by spot electronically.

Another feature of the RNG is that it is always working, even when you’re not playing, including between two consecutive spins, picking hundreds of random numbers per second. Every fraction of a second you delay in hitting the spin button results in a different outcome of the spin. Given all these said, there is no rational reason for a player to do any of the following:

• be upset when someone hits a jackpot on a machine they were just playing (because the player would have hit the spin button at a slightly different time than the winner did);
• choose a machine just because it has not paid anything or has paid very low for a long period (as this does not imply that it will start paying after the player takes it);
• move to another similar machine because the machine that they are playing at either did not pay for a long time or has just paid (as the payback is not distributed uniformly, and the statistical average does not apply to short to medium intervals of spins).

Of course, these possible behaviors do not break any mathematically based optimal strategy of playing slots because such a strategy does not exist. They are just mentioned as useless consequences of fallacious beliefs; the last two actually fall within the Monte Carlo fallacy (also called the gambler’s fallacy). If the player takes any of those actions, there is nothing essentially and practically wrong with that except for their reasoning. The only objective strategy in slots concerns the bankroll and the intended limit of playing time, which are related to each other and amount to safe gambling.

References

Bărboianu, C. (2013). The mathematics of slots: Configurations, combinations, probabilities. Craiova: Infarom.

Bărboianu, C. (2022). Understanding your game: A mathematician’s advice to rational and safe gambling. Târgu Jiu: PhilScience Press.

Harrigan, K. A. (2007). Slot machine structural characteristics: Distorted player views of payback percentages. Journal of Gambling Issues, Vol. 20, 215–234.

Turner, N. E., & Horbay, R. (2004). How do slot machines and other electronic gambling machines really work? Journal of Gambling Issues, Vol. 11.